Introduction
During more than 25 centuries western thinking was dominated by the dualistic paradigm described by Aristotle's syllogism. A statement is true or false, exclusively one of both, and all of intellectual activity consists of evaluating, arguing or refuting the statement. This approach got a boost during Renaissance, where "cartesian" deductive logical and mathematical thinking was considered as the absolute requisite for any kind of scientific, "experimental", reliable thinking.
Apart from its contributions to deductive thinking, this approach is misleading in at least three of its explicitly or implicitly suggested conclusions:
(1) there is no category between true and false;
(2) science and technology are making progress thanks to logical deductions and experimental procedures;
(3) "sciences" which so far are unable to apply the exact, experimental procedure can't be rated as scientifically reliable, and remain in the realm of mythical, obscure, fictitious and unreliable thinking.
During the second part of the 20th century, after the umpteenth deception about the blessings of scientific progress, tentatives towards a more holistic, non-aristotelic approach of reality were launched. This trend is masterly pictured by authors as Fritjof Capra. Many approaches, from postmodernism to New Age, recommend a less dualistic, mutually-exclusive way of thinking. But up to now a central paradigm was not clearly defined. In this essay, integration is proposed as such a paradigm.
Definition
As defined elsewhere, integration can be defined as [1,2]
a process of combination of elements that, at first approach, seem to be incompatible or even conflictuous, but, after a bit of analysis and re-synthesis (leading to reformulation or re-orientation), prove to be rather complementary.
Symbolically this process could be represented by:
(A,B) Æ [A>>A'] & [B>>B'] Æ {A'B'}
where A en B are elements in their primary, "unintegrable" state, that are "retroduced" to their "essential core" [AÆA'] & [BÆB'], what makes them "integrable", and then combined into a new unity {A'B'}. Æ here means "to provoke a certain fact or transformation". and >>here means "to transform into". We use the three kinds of brackets in a different sense: (collection of elements), [process], {integration}.
We would like to introduce the function of Y (Psi) meaning "to be reduced to its essential core", so that:
Y(A) = A'
and v as the inverse function, the "eduction"
A = v(A')
so that A is an eduction of A', meaning that we can come from A' to A by making A' less general.
Likewise we propose to introduce the fundamental function W (Omega) to describe the integrative process in short:
W (A,B)= {A'B'}
To make the indication "a more integrative version" more precise than A' relative to A (A' meaning just "vaguely related to") we propose to introduce the index # meaning "more integrative".
Symbolically, the above statements can be written as
(A,B) Æ [A>>A#]& [B>>B#]Æ {A#B#}
Y(A) = A#
A = v (A#)
W (A,B) = {A#B#}
Assumptions
The paradigm of integration is based upon some assumptions, postulates, some of them conflictuous with the fundamental logical postulates.
1. The probability that a theory is completely true/false, is practically nill
The probability that a theory, an insight, a concept, a hypothesis, an idea, etc. is completed, completely exact and true, is practically inexistent. Each idea, etc. will probably be improved some day. So between "true" and "false" a third category has to be intercalated, being defined as "theories that are far more better than previous theories, but not as perfect as the final theory".
The classical, dualistic, aristotelian-cartesian categories:
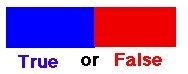
In the integrative approach we discern three categories:

In practice, we could probably put all existing theories, concepts, etc., in the middle category, making both classical logical extreme categories obsolete, i.e. only existing as a theoretical concept, unless we're working with extremely simple data, e.g. natural numbers and other conventional concepts.
Inspired by the diagram, we could, perhaps, represent the presence of the plausibility factor, in discursive intellection, as forming an important part of a sort of continuum as follows:
"FPPPPPPPPPPPPPPPPPPT",
where "F" stands for "false", "P" stands for "more or less plausible" and "T" stands for "true".
The more an outlook is implausible, the closer it stands to the "F" or "false" end of the continuum, and the more an outlook is plausible, the closer it is the "T" or "true" end of the continuum. [Brian Cowan]
As the "plausibility" category is very extended, it seems useful to introduce a measure of plausibility (P). This measure can only be used in a relative sense, i.e. by comparing two or more theories.
Example. If we define TE as the Theories of Einstein, and TN as the Theories of Newton, we can state that:
P(TE) > P (TN)
Or:
Y(TN) = TE
TN = v (TE)
As explained in the General Systems Theory, and Logics, knowledge of any rather complex system presents a progressive development: as with a spiral, each new experience or intellectual confrontation may lead to a more comprehensive conceptualization.
E1(A) Æ a1
a1 + E2(A) Æ a2
a2 + E3(A) Æ a3
generally described as
an-1 + En(A) Æ an
A is a phenomenon, a part of reality to be conceptualized. E is an experience and/or an intellectual communication. E(A) is an experience with phenomenon A , and E1(A), E2(A)... are consecutive experiences. a1, a2, ..., anare consecutive visions, hypotheses about phenomenon A , becoming progressively more integrative. A cyclic scheme could also represent this procedure:
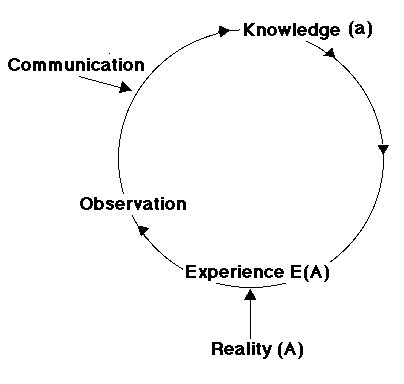
This means that at each given moment, each concept may become more complete, more realistic, more comprehensive, more integrative.
The historically most significant example is the theory of Newton, improved by Einstein. This example is particularly striking because during centuries the theories of Newton were quoted as the illustration par excellence of scientific, aristotelic-cartesian thinking. Let's take Newton's Law of the Addition of Speeds:

Einstein proposed an elaborated formula:
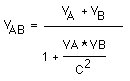
This means that at relatively slow speeds (v << c), the denominator practically equals 1, so we find back Newton's formula. But at high speeds the denominator increases, making the total speed significantly lower than what Newton predicted, and limiting even the maximal speed at the speed of light, c. Newton's formula appears to be a reduction a simplification of Einstein's elaborated formula, but at "normal" speeds on earth it was impossible to discover the inaccuracy of Newton's "simple" formula.
2. The 'complements' operator - the non-existence of contradictions
As there exists more than one category of exactness, the opposition and mutual exclusion of two statements (about the same phenomenon) that are not similar or reduceable to each other, disappear. Besides the fundamental categories equals (=) and is unequal (<>) we should like to introduce a third, much more useful operator: complements (¿)
Where in the traditional approach statements as
psychoanalysis <> behaviourTheory
science <> religion
theoryOfNewton <> unexplainableEvidence
seem very justified, in an integrative approach they are... false, because:
psychoanalysis ¿ behaviourTheory
science ¿ religion
theoryOfNewton ¿ unexplainableEvidence
Hence:
W (psychoanalysis, behaviourTheory, ...) = integrativePsychology
W (science, religion, ... ) = hyperphysics
W (theoryOfNewton, unexplainableEvidence ) = theoryOfEinstein
("Hyperphysics" being the name that Teilhard and Wildiers used as the scientific label for their evolutionary, cosmic and integrative approach).
This second postulate can be formulated another way: the probability that in two statements, which seem mutually exclusive of paradoxical, one is true and the other is false, is much lower than the probibility that both pseudo-conflicting statements are complementary, i.e. true in certain circumstances. Practically speaking: all so called contradictions are most probably complements.
3. An integrative theory is more plausible than its non-integrative elements
The degree of plausibility increases with integration, at least if no logical errors are made. This can be explained by the fact that the plausibility of the integrative view is at least as high of the plausibility of the most plausible of its complementary elements.
So we can state that
P(A#) > P(A)
and, more in detail, if:
W (A1, A2 , A3 , ...) = A#
then:
P(A#) > P(A1)
P(A#) > P(A2)
P(A#) > P(A3)
...
This has a very important consequence: to achieve the highest possible plausibility, one has to integrate. Or, otherwise stated, the Plausibility is the highest with theories that take into account the greatest number of phenomena, the greatest number of arguments.
Graphically represented:

A "proof" based upon the integration paradigm can be made by arguing, mathematically or logically, that the former, non-integrative theories can be reached by an eduction (v) of the integrative theory.
If
W (A1, A2 , A3 , ...) = A#
then the maximal plausibility for A# (replacing the obsolete concepts true and exact) is reached when
A1 = v (A#)
A2 = v (A#)
A3 = v (A#)
i.e. if we can (d)educe each elementary theory from the integrative, by restricting the conditions of applicability or observation. This is a proof, in the scientific meaning of the word, that the integrative theory is (more) true (preferably: plausible) than the non-integrative ones.
This edutive operation can easily be done with Einstein's theory about the addition of velocity, that mathematically can reduced to Newton's formula by putting v as extremely low, so that the denominator practically equals 1, and can be removed in the formula.
Implications. This third assumption has many important implications for science in general, especially for these sciences that are seemingly (still) inaccessible for the exact-scientific method. These consequences apply as well to the curriculum of the studies, as to the structure of scientific papers. In another article we will extend on that topic.
The integrative procedure
1. Introduction
Deduction and induction. The process of integration, leading to the formulation of a new, more plausible hypothesis, is part of the indcution process, which is still unconscious and inaccessible for conscious reasoning. All the Principles of Logic, from Socrates to Descartes and Leibniz, in fact are Principles of Deductive Logic. An Inductive Logic is still to be elaborated. This integrative process can be seen as the kernel of such a paradigm.
In the next scheme the process of thinking is depicted. In intelligent beings, Reality is, at least in part, observed, and out from these observations some general tendencies are abstracted. These are the hyotheses, the knowledge, general rules and laws. The hypothesis formulation process is called induction. From these abstract hypotheses, conclusions can be drawn by logical, deductive thinking. Generally this operation consists in replacing abstract data by concrete numbers, and performing some mathematical transformations. Science is a collection of conscious rules, i.e. operationalized and measurable. Also in exact science, the elaboration of a scientific hypothesis is an intuitive process. In fact, science only controls the "exactness" of the intuitively formulated hypotheses.
In many cases, the hypothesis itself remains hidden in the realm of the unconscious, and is then called intuition. In this case also the deductive process is largely unconscious and intuitive, e.g. art, musical improvisation.
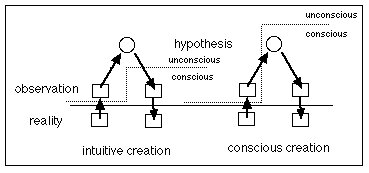
The integration process is the elaboration of a new, more general hypothesis out of some particular hypotheses with limited applicability.
Because it is still largely unconscious, this process can not ye be described in detail, not yet operationalized, and not yet programmed for a computer. All computers are still deductive up to now, although when the possibilities are limited, a pseudo-inductive routine can be elaborated, like in computer chess programs: a mathematical calculation of all possible reactions is made, and a quick statistical evaluation is made of the outcome of each possibility, and then a mathematically guided choice is automatically made.
But although we can't yet describe the process in detail, we can identify several subphases, making the theoretical challenge more realistic, and perhaps coming closer to the long expected discovery of an Inductive Logic. We also will offer some auxiliary tools to enhance this subconscious integrative process.
2. Eduction (v)
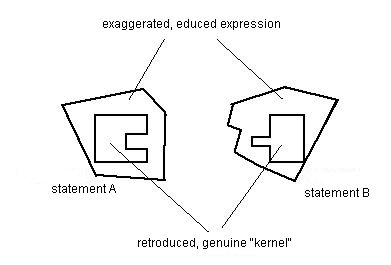
Let's consider two statements, A en B. They seem irreconcilable:
A <> B
But let's suppose that, most probably, both observers were sufficiently intelligent not to be completely wrong, and were observing different situations: different factors elicited different behaviours in the same object. So the different perceptions of the same object are in fact compatible, save for the exaggerate generalization (eduction), unconsciously made in the absence of correcting phenomena, thus making the statements unnecessarily incompatible.
3. Retroduction (Y)
The solution is that both observers retroduce their statements, by adding nuances or limiting conditions, making an integration possible.
We postulate that A ¿ B, and we retroduce A and B to A# and B# by
Y(A) = A# and Y(B) = B#
4. Combination (+)
At this point an integration, now nothing more than a simple combination, will be possible:
W (A, B) = {A#B#}

To perform this integration, several methods seem useful:
- Each observer can be placed in the situation of the other observer, and discover that his statement needs some more nuance.
- The observers can communicate their different approach to each other, believe each other, and by empathy understand the limits of their own experience, and make together an integrative hypothesis satisfying both of them.
- One observer can accept the apparent contradictory statements as complementary, and try to formulate an integration.
5. Auxiliary methods
The intuitive integration probably will be inspired by analogies, and especially by analogies with fundamental features of reality described by the General Systems Theory, and assisted by inductive Logics.
In another article, several auxiliary tools to enhance intuitive integration, are described.
Primitive forms of Integrative Thinking
1. Introduction
If we consider the ways of thinking humans used in history, some difficult questions arise
- During Renaissance, the scientific method of thinking emerged, claiming that a hypothesis only could be accepted as "true" if experimental ebidence cam to support it. How do we explain that, before this time, so much exact science was developed, including Greek mathematics and science, Egyptian and Assyrian geometry, architecture and astronomy. How could, ironically, such a inexact way of thinking, typical for the so-called Dark Middle Ages, develop the laws of exact scientific reasoning?
- What's the difference between Aristotelian dualism and Cartesian dualism?
- Was thinking with revelated insight really so naive and so stupid?
These questions could perhaps receive a beginning of an answer with the following considerations.
2. Intuition and "Revelation" as a primitive form of integration
One could perhaps consider that those "primitive", "unscientific" forms of thinking were in fact kinds of integrative thinking. The most important condition for integrative thinking, i.e. a general knowledge of multiple fields of human experience, was fulfilled. The ancient philosphers, unless nowadays scientists, appeared to be experienced in many diverse "sciences", ranging from mathematics to architecture and the art of war making, from music to medicine, passing through law, politics and astronomy, all in one person. The notion of homo universalis,[3] i.e. someone who knows "everything", was a high ranking qualification until the 17th and even the 18th century. Blaise Pascal (1623-62) is renown as the "last" homo universalis, although I should tend to qualify Teilhard as a modern homo universalis.
This very general, universal intellectual development is a fertile source for integrative thinking. From such a diversified experience and knowledge, the philosopher-scientist tries to formulate for himself hypotheses that fit with his experiences. The control for the validity of such a hypothesis is his intuitive certitude that all important data are explained. The same phenomenon probably occurs with a successful artist: he "feels" that his creations are "right", i.e. an intregration between a series of good separate ideas.
The step from such an intuition towards the honest conviction that one is enlighted by divine revelation, is not far.
The thinking error is not that one conceives such intuitive integartions as plausible, but as absolutely true, because God can't lie.
3. The scientific method of Pierre Teilhard de Chardin
The notion of thought or consciousness moving along a continuum of ever increasing plausibility seems to be compatible with Teilhard de Chardin's view that thought or consciousness gropes its way forward from one approximate conception of reality to another with, on average, later cognitional approximations being more accurate that earlier ones. In this regard, the French Jesuit writes: 'Consciousness, we know, does no more than grope its way forward, one approximation following upon another.' [4] And elsewhere, in a not dissimilar vein, he remarks that 'the history of the living world can be summarised as the elaboration of ever more perfect eyes within a cosmos in which there is always something more to be seen.' [5] Whether these eyes are those of the body or of the mind, their function is always 'to try to see more and better' [6]. So, Teilhard, here, does seem to be, at least in part, talking about consciousness at the thinking level, ever groping it's way, by means of increasingly plausible cognitions, away from falsity towards truth.
Hence I believe that Teilhard was, in large measure, an integrative thinker and theoriser. In this connection, in an essay of his, we read:
'What I wish to offer here is the outcome of my own thinking, expressed in a simple and clarified form so that everyone may be able to understand it without ambiguity, and may criticise and (this is my great hope) correct and amplify it.' [7]
So, to all appearances, the French Jesuit was open to having his outlook, on an ongoing basis, criticised, corrected and amplified with a view to having it continuously nudged forward along the plausibility continuum in the hope that it would ever move closer and closer to the truth.
4. Teilhard and Revelation
His approach. I have, above, used the expression "in large measure" advisedly. My reason for doing so is that that, in my opinion, as regards one area of his outlook, Père Teilhard does, in some measure, and in some sense, believe he stands, from a knowledge standpoint, at the truth end of the plausibility continuum. And this one area, as I have said elsewhere, is that of his religious faith which, to his mind, contains indubitable certitudes revealed by God to humanity by way of scripture and the Church.
Thus we find Teilhard referring to 'the revealed knowledge' which is 'afforded us by the Catholic faith' and 'which is richer and more exact' than knowledge 'in the field of pure empirical science.' [8] In the expression "richer and more exact", we can probably read "truer and more accurate". So, in the mind of the French Jesuit, the knowledge that comes to us by way of divine revelation is, in some sense, a kind of knowledge that outranks ordinary knowledge in terms of its truth value.
For Teilhard, when, by way of divine revelation, we receive 'from on high', from God, 'a reply' to our religious questioning, 'we in some way enter the order of certainty' and leave behind 'the scientific framework of "hypothesis".' [9] So, once again we encounter the notion that divinely revealed knowledge significantly surpasses ordinary knowledge as regards its truth value.
One 'lesson of revelation', in the eyes of the French Jesuit, is the religious teaching that there is a cosmic Christ, 'a Word who makes himself incarnate.' [10] The knowledge which this religious teaching affords, in the opinion of Teilhard, is a knowledge which is at the truth end of the plausibility continuum.
So, for Teilhard, how would his certainty about the reality of a cosmic Christ square with Kris' s first postulate that there is very little probability, in the overwhelming majority of cases, that a theory is entirely true. My suspicion is that the French Jesuit would agree with the postulate, but also maintain that his knowledge of the cosmic Christ is a sort of special knowledge, a knowledge that transcends theory because it is revealed knowledge. Further, my hunch is that Teilhard would also claim that because this knowledge is a special, transcendent kind of knowledge it is exempt from the normal condition of ongoing self-correction that is invariably associated with theory.
Criticism. What are we to think of Teilhard's view about these two levels of knowledge, an ordinary and perpetually self-correcting level based on experience, and a super-ordinary changelessly true level based on divine revelation? Is this view viable over the long term? No doubt these questions are among those that are being pondered by those who concern themselves with carrying out the task, set to them by the French Jesuit, of criticising, correcting and amplifying his thought.
My own personal opinion is that Teilhard's "two level" approach may not be viable over the long term. Why? Well, as I have said before, what was once taken to be inerrant truth based on Scripture has turned out to be mistaken:
- Historically, texts in the Bible, said to be divinely revealed, have been used to justify claims that the universe was created in six days, that the universe began to exist around the year 4000 B. C. E.,
- that the cause of evil is a culpable trespass on the part of the first two humans on earth,
- that the sun orbits the earth, and
- that child abuse and slavery are morally acceptable.
I think that when slavery (and the submission of the woman to her husband) seem to be acceptable for the Church Fathers, paedophily was considered as very rejectable from the very beginning. Nevertheless, ons could add to this list:
- the degradation of sexuality, only acceptable for men "not able to vow themselves to celibacy".
- the dogm of the Virgin-Mother, an offense for every mother and woman
- the acceptance of death penalty, the benediction of war, the acceptance of revealed arguments against scientific and experimental evidence, etc.
Now, if all of these "revelations" were mistaken, I ask myself, what guarantee do we have that the "revelation" of a cosmic Christ is valid, is not also mistaken?
Teilhard, as he tells us, looks largely to 'the Christogenesis of St. Paul and St. John' for support of his view that there is a cosmic Christ. But, I ask myself, how do I know that St. Paul and St. John were not mistaken on this matter?
It does seem to be the case that St. Paul was mistaken on the morality of slavery [at Ephesians 6: 5-9 and Colossians 3: 22-24], and this mistake, on his part, was used by pro-slavery persons and groups, in the 18th and 19th centuries, in their disputes with the abolitionists. As we know, the abolitionists eventually prevailed, and it is now generally admitted that, on the question of slavery, Paul was mistaken. Might he also be mistaken as to the reality of a cosmic Christ? I answer: "Yes, this is quite possible." Others, of course, answer: "No, this is not possible." Perhaps, only time will tell which response is more nearly correct.
I think that, (1) if we consider revelation not as a direct intervention of a Superbeing into the natural evolution, but as a message that can be "read" in nature and reality because it was there since the very moment of Creation, and (2) if we consider integrative thinking, including its primitive forms intuition and "feeling a revelation" as yielding plausibility in stead of absolute truth, we can still trust in integration.
[1] Roose, K., 1980, Ontwerp voor een Integratieve Psychologie, Gent.
[2] Roose, K. & Van Brandt, B., 1985, Het geheim van het geluk, Kluwer, Antwerpen-Deventer
[3] Beckers, Danny. ""Pieter Nieuwland (1764-1794): natural philosopher, mathematician, and poet"; mathematical societies in the Netherlands and the ideal of the Homo Universalis" De Achttiende Eeuw, 33, 1 (2001): 3-20
[4] P. Teilhard de Chardin, 'The Evolution of Chastity', in 'Toward the Future' (Harvest Book, 1975), p. 60.
[5] P. Teilhard de Chardin, 'The Phenomenon of Man' (Fountain Books, 1977), p. 35.
[6] P. Teilhard de Chardin, 'Phenomenon', p. 35.
[7] P. Teilhard de Chardin, 'The New Spirit', in 'The Future of Man' (Harper & Row, 1969), p. 85
[8] P. Teilhard de Chardin, 'The Phenomenon of Man', in ''The Vision of the Past' (Collins, 1966), p. 161 (In footnote # 1).
[9] P. Teilhard de Chardin, 'Outline of a Dialectic of Spirit', in 'Activation of Energy' (Harvest Book, 1970), p. 148.
[10] P. Teilhard de Chardin, 'Outline of a Dialectic of Spirit', in 'Activation', p. 148. (8) 'Phenomenon', p. 325.