Science is a method to acquire reliable certitude about the statements, inductions and deductions we make while thinking about reality.
Concerning the "methodology", there are, generally speaking, two ways of applying science: the exact method, and the plausibility method.
1. The exact method, Exact Science (ES)
Before Renaissance, people made spontaneous associations, based upon vague intuitions. The intuitions of "sages" and "philosophers" were considered as more reliable, and influenced, by their authority, the concepts of other people.
During the Renaissance the "exact" method was progressively developed. Hypotheses were only accepted as reliable if they reposed upon exact measures, and were controlled by measurable deductions. This happened during the Reanaissance, because measuring tools became progressively available, and the general cultural attitude became more non-authoritarian. The exactness of the "science" proved less reliable than hoped for at the beginning: even Newton's mechanics, the symbol par excellence of exact science, had to be corrected by Einstein.
In fact, from a science psychology standpoint, what happened during Renaissance? Probably several psychological and social factors coincided, but two seem to be paramount:
1. the availbaility of new observational tools, from microscope (Robert Hooke, Antony van Leeuwenhoek) to telescopes.
2. a non-authoritarian attitude towards knowledge in general. The psychological aspect of the Renaissance is perhaps best described as a kind of social puberty, rejecting all kinds of moral authority. The anatomical discoveries by Vesalius , refuting one millenary of Galenic medical dogmas, were just done with the naked eye. The only thing that was needed was the attitude.
These tools yielded an impressive amount of hitherto unknown data, changing completely the view of reality and falsifying many traditional theories. Furthermore, the increasing number of discoveries elicited a kind of virtual circle, enhancing the attitude --and multiplying the discoveries.
But the exact method has, besides its innumerable advantages, two important limitations:
- It is, in fact, not a tool for developping science, but a tool for controlling the hypotheses, once formulated. These hypotheses are still formulated on an intuitive basis.
- It is limited to domains where measures can be made. There are, of course, a certain number of fields where we can expect that measuring tools will be developped in the near future. So we could wait. But very important domains, including psychology, politics, philosophy, ethics, religion, (and, paradoxically, the fundamental structure of matter and cosmos) just can't wait, and measuring tools are not yet in sight.
2. The integrative method, Integrative Science (IS)
Although the supporters of the exact scientific (ES) method claim that it is a pity but we have no other choice than to wait, because those domains still remain in the field of myths and confabulations, during the 20th centrury another method of scientific thinking was progressively developped, without having a name in the beginning. Teilhard and Whitehead were its first brilliant students, and Capra perhaps the first theorist. This method is called with several names, not always covering exactly the same approach, including holistic, postmodern, non-dual. The "plausibility method" seems to me perhaps the most appropriate.
This method starts with a definition of the notion of integration. This procedure is described in detail on another page. This notion presupposes that every intuitive hypothesis that seems to be confirmed during a certain period, most probably contains at least a part of truth, or --formulated the other way-- the probability that it should be partially right, at least in certain circumstances, is greater than then probability that it should be complete wrong or unreliable. This implies that conceptual conflicts not have to be interpreted as an indication that one hypothesis is "right", all the other being "wrong", but rather that the formulation of the hypothesis probably is inexact to a certain degree. The inexactness most probably is due to a unprecise connection between cause and effect. If it are theories, we call this over-generalization, if it are projects, we call this over-concretization, which means that the person thinks that there is only one possibility to achieve his goal.
This problem is not typical for the plausibility method. The error Newton made was in fact exactly the same: he supposed that there were no other possibilities than the wide range of observations with speed he made. In his days high speeds and microscopic objects were unobservable. So his formulas were only true within a limited range of applications: only with relatively big objects moving at relatively low speed.
In fact, the fundamental thing the exact scientific method contributed to the reliability of human knowledge, was one method to limit the margin of inaccuracy. Not the impressive mathematics are the contribution of the renaissancistic scientific revolution: they existed already, to a large extent, in ancient times, enabling the exploits of Pythagoras, Euclid and Archimedes. Nor was it a better kind of induction: even Einstein had to develop his theorems by intuition. Mathematics and the other methods of exact deduction are no guarantee for the reliability of science: even with the most exact mathematical methods, conclusions derived from Newton's laws are highly inexact, as soon as they are applied on other objects and speeds than those observable in Newton's days. In fact, modern science is just a way to control hypotheses, not to develop them. The development is still intuitive, but now within narrowed limits. The integrative method is just another method for narrowing those limits, but this time applicable within inexact and immeasurable domains --as long as they remain so.
Some Characteristics of Integrative Science (IS)
Integrative, post-modern science seems to be different form exact, modern science on several aspects. But a closer look often will reveal that those differences are not that fundamental as seemed to be at first glance. Most of the criticisms on integrative science are based upon a caricature or one-sided description of IS. Several criticism probably are generated by the fact that most "scientists" are in fact not creative at all: they just work in the safe field between "proved" hypothesis and application. They seldom leave the field of deduction, whereas scientific progress always implies inductive working. Moreover, the greatest scientific thinkers weren't those with the most impressive diploma, and many a creative thinker was rebutted by academic authorities.
The rules of IS are, in fact, very strict and demanding, often more demanding than for ES. Moreover, they will, if applied on a larger scale, probably totally change our scientific and academic structures and publications. Integration is neither the same as synthesis, compromise, consensus, nor is it simple intuition, or a kind of greatest common divisor.
1. Back to intuition?
A first criticsm is that by rejecting the benifits of ES, one goes back to the intuition paradigm of the dark Middle Ages. Intuition, often authenticated by the authority of philosophical Wisdom and Divine revelation, couldn't prevent aberrations as those exposed by Vesalius and Copernicus.
This approach is deceiving. Modern science only provided a controlling tool --exact observation and controlled experiment. Intuition --the core of hypothesis development-- was never replaced by something else. But, confronted with exact data, the margin for intuition was much more restricted.
Thus, IS is not refuting ES, it just adds something. ES has to be continued as before. But for the great number of domains, hitherto inaccessible for science, another controller of intuition is provided: integration. Rather than advocating a return to free intuition, ES is offering a technique for scientific progress on those most important fields of life --from psychology to politics, from cosmology to religion, from artistic creativity to the secret of happiness. Nevertheless, it is most probable that ES may contribute something to ES, where ES heavily relies on intuition: IS offers a method for refining intuition.
Moreover the plausibility method doesn't try to replace the exact method, but to complement it. One of the constituents can be an exact scientific hypothesis, so the plausibility of an integrative hypothesis becomes higher than the plausibility of its scientific constituent(s).
2. To specialize or not to specialize?
One of the most demanding conditions is that an integrative thinker has to start from the largest possible observational field, as multidisciplinarily as possible. Teilhard -working from paleontology and evolution towards sociology and religion- and Whitehead -starting as a mathematician and ending up as a philosopher- were perhaps the most brilliant forerunners, who applied, rather intuitively and avant la lettre than consciously- the integrative method. This makes their conclusions highly plausible.
The Plausibility is highest with theories that take into account the greatest number of phenomena, the greatest number of arguments.
Graphically represented:

As we will discuss in our final conclusions, a most universal applicability, is the fundamental rule that, in IS, replaces exact measuring of ES. This is a very demanding condition for Integrative Scientists, and will be the most difficult obstacle to develop academic curricula that respect the requirements of Integrative Science.
3. True or plausible?
The conclusions of integrative science are never true in the exact scientific meaning, but just plausible. The plausibility increases with the number of constituents, not only with the first thinking process, but with every subsequent integration.
The so-called truth in exact thinking is a very fallacious notion. Although since more than a century it is clear that even the most respectable laws of Exact Science has to be revised, the general impression prevails that the laws of science are eternal, and their deductions absolutely reliable. Revisions may occur from time to time, but they are rather the exception.
Integrative science adopts another stance. It considers thinking as a circular, or rather a spiral process, with even more plausibility at each circular movement.
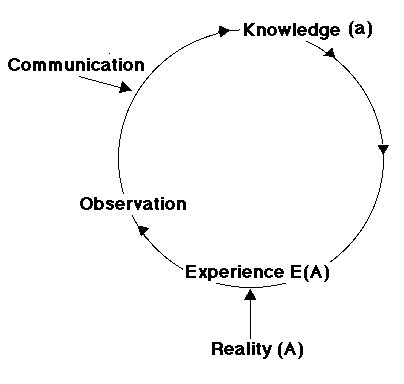
This means that at each given moment, each concept may become more complete, more realistic, more comprehensive, more integrative. It considers as rather exceptional that an integrative hypothesis should remain unrevised for a long period of time.
The plausibility of the intregrative concepts may appear less "exact" than the "truth" of ES. This is probably a false impression: the exact laws of Newton, and also those of Einstein, revised by Quantum Mechanics, the changing value of the "constant" speed of light, and the Quantum Entanglement of particles, prove to be much less reliable than when they were enthousiastically proposed. Anyway, we never can be sure in advance of the inexactness of scientific hypotheses. Plausibility and Hypotheses are just more honest and modest terms than Truth and Laws, and should perhaps be introduced in Exact Science as well.
4. A novel Way of Thinking?
Another criticism is that plausibility should be a novel way of thinking, where the "exact natural sciences". Some arguments contravene this statement.
1. The ancient, "pre-modern" way of thinking, amply used by ancient scientists and --to a lesser degree-- during Middle Ages, was in fact much more analogous to Integrative thinking. The philosophers and scientists --most often the same people-- of ancient times in fact used the integrative method, and controlled the margin of inaccurateness by studying many different sciences and fields of human knowledge --and even art. One could state that they went to the limits of what an intellectual could perform in those days. The major difference between postmodern and the premodern thinking, is the enormous amount of available data, including the contributions of Exact Science.
2. Integrative thinking is the way the brain thinks. In fact, exact thinking is highly artifical and can't, even by skilled scientists, nearly never be performed without the assistance of paper-and-pencil, or a computer. In fact, man can't even calculate, hence we start memorizing, at a very early age, the multiplication tables. And a slightly complex logical problem, with a number of negations and suggestive ambiguities, predictably leads to logical errors.
In fact, nature couldn't take the risk to produce an exactly functioning brain, for some vital reasons, including: (1) every day a certain number of brain cells die to never be replaced. A way of thinking, where each precise detail is indispensable and extremely important should, with a biological brain, lead to catastrophes. (2) man are most often confronted with new, unknown situations and problems, where their accumulated knowledge and experience doesn't provide an immediate answer. An "exact" brain should be highly inappropriate to cope with life.
Therefor, nature opted for associative thinking. This way of thinking is highly imprecise, but incredibly sppedy. Plausibility is attained by combining tens and tens of associations that arise within instants. The common field, that is covered by most assciations, is coinsidered as the most plausible.
An example to illustrate this. If somebody should ask us "how much is 367 * 629?" we probably should come into trouble. But if the person adds "the right answer is 834.885.177" we probably should immediately reply "that is wrong". How can we be so certain that this is not the right answer, even if we don't know the right one? Because, by associatio, we "feel" that the right answer should be something between 180.000 (300 * 600) and 280.000 (400 * 700) or between 10.000 (100*100) and 1.000.000 (1.000 * 1.000). Moreover, you can't have a result with 9 digits by multiplying two numbers of 3 digits
The ES is nothing special for us: it emanates from natural thinking. Computer thinking and exact deductive thinking in general is highly artificial.
Some Modalities of Integrative Science
1. A fundamental attitude. Integrative science presupposes some general attitrudes towards self, other people and existence in general, to enable a constructive dialogue. Those rules include adagiums as: Eevery conflict is a pseudo-comflict: with appropriate Florian
A "proof" based upon the integration paradigm can be made by arguing, mathematically or logically, that the former, non-integrative theories can be reached by an eduction (v) of the integrative theory.
If
W (A1, A2 , A3 , ...) = A#
then the maximal plausibility for A# (replacing the obsolete concepts true and exact) is reached when
A1 = v (A#)
A2 = v (A#)
A3 = v (A#)
i.e. if we can (d)educe each elementary theory from the integrative, by restricting the conditions of applicability or observation. This is a proof, in the scientific meaning of the word, that the integrative theory is (more) true (preferably: plausible) than the non-integrative ones.
This edutive operation can easily be done with Einstein's theory about the addition of velocity, that mathematically can reduced to Newton's formula by putting v as extremely low, so that the denominator practically equals 1, and can be removed in the formula.
Implications. This third assumption has many important implications for science in general, especially for these sciences that are seemingly (still) inaccessible for the exact-scientific method. These consequences apply as well to the curriculum of the studies, as to the structure of scientific papers. In another article we will extend on that topic.
Transcend or refute
The integrative procedure
1. Introduction
Deduction and induction. The process of integration, leading to the formulation of a new, more plausible hypothesis, is part of the indcution process, which is still unconscious and inaccessible for conscious reasoning. All the Principles of Logic, from Socrates to Descartes and Leibniz, in fact are Principles of Deductive Logic. An Inductive Logic is still to be elaborated. This integrative process can be seen as the kernel of such a paradigm.
In the next scheme the process of thinking is depicted. In intelligent beings, Reality is, at least in part, observed, and out from these observations some general tendencies are abstracted. These are the hyotheses, the knowledge, general rules and laws. The hypothesis formulation process is called induction. From these abstract hypotheses, conclusions can be drawn by logical, deductive thinking. Generally this operation consists in replacing abstract data by concrete numbers, and performing some mathematical transformations. Science is a collection of conscious rules, i.e. operationalized and measurable. Also in exact science, the elaboration of a scientific hypothesis is an intuitive process. In fact, science only controls the "exactness" of the intuitively formulated hypotheses.
In many cases, the hypothesis itself remains hidden in the realm of the unconscious, and is then called intuition. In this case also the deductive process is largely unconscious and intuitive, e.g. art, musical improvisation.
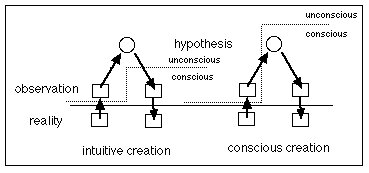
The integration process is the elaboration of a new, more general hypothesis out of some particular hypotheses with limited applicability.
Because it is still largely unconscious, this process can not ye be described in detail, not yet operationalized, and not yet programmed for a computer. All computers are still deductive up to now, although when the possibilities are limited, a pseudo-inductive routine can be elaborated, like in computer chess programs: a mathematical calculation of all possible reactions is made, and a quick statistical evaluation is made of the outcome of each possibility, and then a mathematically guided choice is automatically made.
But although we can't yet describe the process in detail, we can identify several subphases, making the theoretical challenge more realistic, and perhaps coming closer to the long expected discovery of an Inductive Logic. We also will offer some auxiliary tools to enhance this subconscious integrative process.
2. Eduction (v)
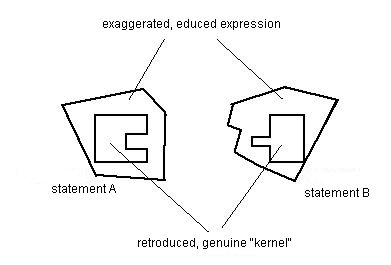
Let's consider two statements, A en B. They seem irreconcilable:
A <> B
But let's suppose that, most probably, both observers were sufficiently intelligent not to be completely wrong, and were observing different situations: different factors elicited different behaviours in the same object. So the different perceptions of the same object are in fact compatible, save for the exaggerate generalization (eduction), unconsciously made in the absence of correcting phenomena, thus making the statements unnecessarily incompatible.
3. Retroduction (Y)
The solution is that both observers retroduce their statements, by adding nuances or limiting conditions, making an integration possible.
We postulate that A ¿ B, and we retroduce A and B to A# and B# by
Y(A) = A# and Y(B) = B#
4. Combination (+)
At this point an integration, now nothing more than a simple combination, will be possible:
W (A, B) = {A#B#}

To perform this integration, several methods seem useful:
- Each observer can be placed in the situation of the other observer, and discover that his statement needs some more nuance.
- The observers can communicate their different approach to each other, believe each other, and by empathy understand the limits of their own experience, and make together an integrative hypothesis satisfying both of them.
- One observer can accept the apparent contradictory statements as complementary, and try to formulate an integration.
5. Auxiliary methods
The intuitive integration probably will be inspired by analogies, and especially by analogies with fundamental features of reality described by the General Systems Theory, and assisted by inductive Logics.
In another article, several auxiliary tools to enhance intuitive integration, are described.
Historical Precursors of Integrative Thinking
1. Introduction
If we consider the ways of thinking humans used in history, some difficult questions arise
- During Renaissance, the scientific method of thinking emerged, claiming that a hypothesis only could be accepted as "true" if experimental ebidence cam to support it. How do we explain that, before this time, so much exact science was developed, including Greek mathematics and science, Egyptian and Assyrian geometry, architecture and astronomy. How could, ironically, such a inexact way of thinking, typical for the so-called Dark Middle Ages, develop the laws of exact scientific reasoning?
- What's the difference between Aristotelian dualism and Cartesian dualism?
- Was thinking with revelated insight really so naive and so stupid?
These questions could perhaps receive a beginning of an answer with the following considerations.
2. Intuition and "Revelation" as a primitive form of integration
One could perhaps consider that those "primitive", "unscientific" forms of thinking were in fact kinds of integrative thinking. The most important condition for integrative thinking, i.e. a general knowledge of multiple fields of human experience, was fulfilled. The ancient philosphers, unless nowadays scientists, appeared to be experienced in many diverse "sciences", ranging from mathematics to architecture and the art of war making, from music to medicine, passing through law, politics and astronomy, all in one person. The notion of homo universalis,[3] i.e. someone who knows "everything", was a high ranking qualification until the 17th and even the 18th century. Blaise Pascal (1623-62) is renown as the "last" homo universalis, although I should tend to qualify Teilhard as a modern homo universalis.
This very general, universal intellectual development is a fertile source for integrative thinking. From such a diversified experience and knowledge, the philosopher-scientist tries to formulate for himself hypotheses that fit with his experiences. The control for the validity of such a hypothesis is his intuitive certitude that all important data are explained. The same phenomenon probably occurs with a successful artist: he "feels" that his creations are "right", i.e. an intregration between a series of good separate ideas.
The step from such an intuition towards the honest conviction that one is enlighted by divine revelation, is not far.
The thinking error is not that one conceives such intuitive integrations as plausible, but as absolutely true, because God can't lie.
3. The scientific method of Pierre Teilhard de Chardin
The notion of thought or consciousness moving along a continuum of ever increasing plausibility seems to be compatible with Teilhard de Chardin's view that thought or consciousness gropes its way forward from one approximate conception of reality to another with, on average, later cognitional approximations being more accurate that earlier ones. In this regard, the French Jesuit writes: 'Consciousness, we know, does no more than grope its way forward, one approximation following upon another.' [4] And elsewhere, in a not dissimilar vein, he remarks that 'the history of the living world can be summarised as the elaboration of ever more perfect eyes within a cosmos in which there is always something more to be seen.' [5] Whether these eyes are those of the body or of the mind, their function is always 'to try to see more and better' [6]. So, Teilhard, here, does seem to be, at least in part, talking about consciousness at the thinking level, ever groping it's way, by means of increasingly plausible cognitions, away from falsity towards truth.
Hence I believe that Teilhard was, in large measure, an integrative thinker and theoriser. In this connection, in an essay of his, we read:
'What I wish to offer here is the outcome of my own thinking, expressed in a simple and clarified form so that everyone may be able to understand it without ambiguity, and may criticise and (this is my great hope) correct and amplify it.' [7]
So, to all appearances, the French Jesuit was open to having his outlook, on an ongoing basis, criticised, corrected and amplified with a view to having it continuously nudged forward along the plausibility continuum in the hope that it would ever move closer and closer to the truth.
4. Other great Western thinkers, including Hegel and Whitehead, intuitively used integrative thinking, and advanced some theories, e.g. Hegel's dialectic, that seem to announce Integrative Thinking. Also Wilber, with his concept of Integral Thinking, comes close to integrative thinking, although he just creates an "integral context", enabling integrative thinking by approaching reality from 4 viewpoints (interior/exterior, individual/social) without introducing the integration procedure.
[1] Roose, K., 1980, Ontwerp voor een Integratieve Psychologie, Gent.
[2] Roose, K. & Van Brandt, B., 1985, Het geheim van het geluk, Kluwer, Antwerpen-Deventer
[3] Beckers, Danny. ""Pieter Nieuwland (1764-1794): natural philosopher, mathematician, and poet"; mathematical societies in the Netherlands and the ideal of the Homo Universalis" De Achttiende Eeuw, 33, 1 (2001): 3-20
[4] P. Teilhard de Chardin, 'The Evolution of Chastity', in 'Toward the Future' (Harvest Book, 1975), p. 60.
[5] P. Teilhard de Chardin, 'The Phenomenon of Man' (Fountain Books, 1977), p. 35.
[6] P. Teilhard de Chardin, 'Phenomenon', p. 35.
[7] P. Teilhard de Chardin, 'The New Spirit', in 'The Future of Man' (Harper & Row, 1969), p. 85